SCIP-Jack
SCIP-Jack is a software package for the classic Steiner tree problem in graphs,
and fourteen related problems, such as the prize-collecting Steiner tree problem,
or the maximum-weight connected subgraph problem.
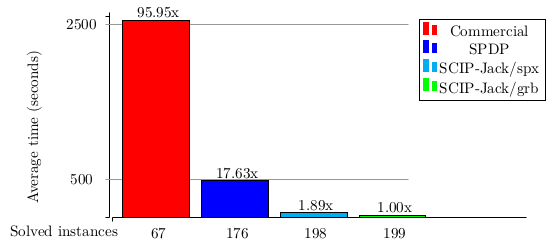
SCIP-Jack is currently the fastest solver for almost all of these fifteen problem classes, including the Steiner tree problem in graphs, the prize-collecting Steiner tree problem, and the maximum-weight connected subgraph problem.
It can typically compute minimum Steiner trees even for large-scale graphs with several hundred thousand edges within minutes.
| 10/May/2018 | SCIP-Jack achieves top rankings in all three tracks of the PACE Challenge 2018, dedicated to fixed-parameter tractable Steiner tree instances: 2nd place in Track A (exact, bounded number of terminals), 1st place in Track B (exact, bounded tree-width), 3rd place in Track C (heuristic). |
| 02/December/2021 | SCIP-Jack 2.0 released (as part of SCIP Optimization Suite 8.0). Major improvements across most problem classes, especially for Steiner tree problem in graphs and prize-collecting Steiner tree problem. |
| 06/July/2022 | The PhD thesis in which SCIP-Jack was developed wins the EURO Doctoral Dissertation Award. | 07/September/2022 | The PhD thesis in which SCIP-Jack was developed wins the GOR Dissertation Award. | 12/September/2022 | The PhD thesis in which SCIP-Jack was developed is a finalist of the INFORMS George B. Dantzig Dissertation Award. |
The current version of SCIP-Jack is 2.0. Due to a licence change of SCIP, SCIP-Jack will not be available anymore as part of the SCIP Optimization Suite. It can still be obtained on request. Please contact Daniel Rehfeldt.
See the INSTALL file in the SCIP-Jack directory.
The default installation uses SoPlex as LP-solver for SCIP-Jack, but it is recommended to use a commerical LP-solver such as CPLEX, Gurobi, or Xpress whenever possible. Note that SCIP-Jack 2.0 was delevoped while using CPLEX (version 12.10) as LP-solver, so the best results can probably be achieved with CPLEX (12.10) as LP-solver.SCIP-Jack can read the .stp and .gr file formats.
bin/stp -f filename.stp on the command line
bin/stp -f filename.stp -s settings/write.set on the command line.
To run a SCIP-Jack binary compiled by CMake, replace 'stp' by 'scipstp' in the above description, and use the folder /build/bin/Release instead of /applications/STP/bin.
Please include one of the following references if you use SCIP-Jack for your work (depending on which problem class you consider):
Steiner tree problem in graphs:
D. Rehfeldt,T. Koch: Implictions, conflicts, and reductions for Steiner trees.
Mathematical Programming, 2023, 197, pages 903-966, DOI: https://doi.org/10.1007/s10107-021-01757-5
BibTeX
Prize-collecting Steiner tree problem:
D. Rehfeldt,T. Koch: On the Exact Solution of Prize-Collecting Steiner Tree Problems.
INFORMS Journal on Computing, 2021, published online first, DOI: https://doi.org/10.1287/ijoc.2021.1087
BibTeX
Maximum-weight connected subgraph problem:
D. Rehfeldt,T. Koch: Combining NP-Hard Reduction Techniques and Strong Heuristics in an Exact Algorithm for the Maximum-Weight Connected Subgraph Problem.
SIAM Journal on Optimization, 2019, 29(1), pages 369–398, DOI: https://doi.org/10.1137/17M1145963
BibTeX
Other problem classes:
D. Rehfeldt, Y. Shinano, T. Koch: SCIP-Jack: An exact high performance solver for Steiner tree problems in graphs and related problems.
Modeling, Simulation and Optimization of Complex Processes, HPSC 2018, Hans Georg Bock, Willi Jäger, Ekaterina Kostina, Hoang Xuan Phu (Eds.), ISBN: 978-3-030-55240-4
BibTeX
Parallelization extensions of SCIP-Jack:
D. Rehfeldt, Y. Shinano, T. Koch: Building Optimal Steiner Trees on Supercomputers by Using up to 43,000 Cores.
Integration of Constraint Programming, Artificial Intelligence, and Operations Research, CPAIOR 2019, Louis-Martin Rousseau, Kostas Stergiou (Eds.), ISBN: 978-3-030-19212-9
Lecture Notes in Computer Science Vol. 11494
BibTeX
SCIP-Jack is distributed under the ZIB Academic License. You are allowed to retrieve SCIP-Jack as a member of a non-commercial and academic institution. For commercial use or support please contact I²DAMO GmbH.
For further questions, or in case of bugs/problems with SCIP-Jack, please contact Daniel Rehfeldt.
Steiner tree problems in graphs,
Steiner arborescence problems (directed Steiner tree problem),
rectilinear Steiner minimum tree problems (see note below),
node-weighted Steiner tree problems,
prize-collecting Steiner tree problems,
rooted prize-collecting Steiner tree problems,
maximum-weight connected subgraph problems,
rooted maximum-weight connected subgraph problems,
maximum-weight connected subgraph problems with budget constraints,
partial-terminal node-weighted Steiner tree problems,
degree-constrained Steiner tree problems,
group Steiner tree problems,
full Steiner tree problems,
partial-terminal Steiner tree problems,
hop-constrained directed Steiner tree problems.
For Euclidean Steiner tree problems and rectilinear Steiner tree problems, it is recommended to use the full Steiner tree generation provided by GeoSteiner and solve the resulting Steiner tree problem in graphs with SCIP-Jack. Many large benchmark instances that cannot be solved by the default GeoSteiner solver in one week can be solved by SCIP-Jack within minutes in this way. Including Euclidean Steiner tree instances with 100 thousand points in the plane.
A collection of well-known Steiner tree test-sets can be found in the SteinLib. See also 11th DIMACS Challenge for additional benchmark instances.